Linear Regression with Adam Optimizer
Adam is one more optimization algorithm used in neural networks. It is based on adaptive estimates of lower-order moments. It has more hyper-parameters than classic Gradient Descent to tune externally
Good default settings for the tested machine learning problems are:
- α = 0.001, // learning rate. We have already seen this one in classic Gradient Descent.
- β1 = 0.9,
- β2 = 0.999
- eps = 10−8.
Values on the right-hand side are proposed in the paper. However, you should tune them on your data, also experiment with batch size and other parameters which may influence the Adam parameters.
Algorithm
Let's look at original algorithm and then try to implement it in the code.
All operations on vectors are element-wise. With β1t and β2t
we denote β1 and β2 to the power of t.
Require: α: Stepsize
Require: β1, β2 ∈[0,1): Exponential decay rates for the moment estimates
Require: f(θ): Stochastic objective function with parameters θ
Require: θ0: Initial parameter vector
m0 ← 0 (Initialize 1st moment vector)
v0 ← 0 (Initialize 2nd moment vector)
t ← 0 (Initialize timestep)
while θt not converged do
t ← t + 1
gt ← ∇θft (θt−1) (Get gradients w.r.t. stochastic objective at timestep t)
mt ← β1 · mt−1 + (1−β1) · gt (Update biased first moment estimate)
vt ← β2 · vt−1 + (1−β2) · g2t (Update biased second raw moment estimate)̂
mt ← mt / (1−βt1) (Compute bias-corrected first moment estimate)̂
vt ← vt / (1−βt2) (Compute bias-corrected second raw moment estimate)
θt ← θt−1−α·̂mt/(√̂vt +eps) (Update parameters)
end while
return θt (Resulting parameters)
At the last line we update parameters based on long chain of formulas which incorporate gradient and moments.
Implementation
Changes to existing library
In order to implement Adam for multi-layer neural network with backpropogation we will need to translate above algorithm to
linear algebra and Tensor API that we wrote in previous articles. Apart from that we would need to
add additional state to Layer type:
case class Layer[T](
w: Tensor[T],
b: Tensor[T],
f: ActivationFunc[T] = ActivationFuncApi.noActivation[T],
units: Int = 1,
state: Option[OptimizerState[T]] = None // additional property for an optimizer
)
We assume that any optimizer may bring its own state apart of the usual weight and bias matrices, so we model new property as trait and add implementation for Adam:
sealed trait OptimizerState[T]
case class AdamState[T](
mw: Tensor[T], // 1st moment equal in shape to weight
vw: Tensor[T], // 2nd moment equal in shape to weight
mb: Tensor[T], // 1st moment equal in shape to bias
vb: Tensor[T] // 2nd moment equal in shape to bias
) extends OptimizerState[T]
We also need to initialise this state properties with zeros. For that, we extend layer construction code to let the optimizer type class to init its properties.
First, we change add method in the Sequential type:
def add(layer: LayerCfg[T]): Sequential[T, U] =
copy(layerStack = (inputs) => {
val currentLayers = layerStack(inputs)
val prevInput = currentLayers.lastOption.map(_.units).getOrElse(inputs)
val w = random2D(prevInput, layer.units)
val b = zeros(layer.units)
// new line to init state for the chosen optimizer
val optimizerState = optimizer.initState(w, b)
(currentLayers :+ Layer(w, b, layer.f, layer.units, optimizerState))
})
Optimizer trait now gets additional method:
def initState[T: ClassTag: Numeric](
w: Tensor[T], b: Tensor[T]
): Option[OptimizerState[T]] = None
Adam implementation for initState:
override def initState[T: ClassTag: Numeric](
w: Tensor[T],
b: Tensor[T]): Option[OptimizerState[T]] =
Some(AdamState[T](w.zero, w.zero, b.zero, b.zero))
Tensor.zero method creates new tensor with zeros using the same shape as original tensor.
Also, we need to keep Adam hyper-parameters somewhere. Let's create OptimizerCfg class and Adam extension in it.
We could design custom configuration nicely, for example, using traits, but I have decided to make it "dirty" at the moment:
case class OptimizerCfg[T: ClassTag: Fractional](
learningRate: T,
clip: GradientClipping[T] = GradientClippingApi.noClipping[T],
adam: AdamCfg[T]
)
case class AdamCfg[T: ClassTag](b1: T, b2: T, eps: T)
Update Weights using Adam
We now have all abstraction in place as well as all parameters to implement Adam optimizer.
In fact, first part to calculate gradient (partial derivative) will be the same as in classic gradient descent algorithm.
Second part will be Adam's own stuff:
override def updateWeights[T: ClassTag](
layers: List[Layer[T]],
activations: List[Activation[T]],
error: Tensor[T],
c: OptimizerCfg[T],
timestep: Int
)(using n: Fractional[T]): List[Layer[T]] =
val AdamCfg(b1, b2, eps) = c.adam
def correction(gradient: Tensor[T], m: Tensor[T], v: Tensor[T]) =
val mt = (b1 * m) + ((n.one - b1) * gradient)
val vt = (b2 * v) + ((n.one - b2) * gradient.sqr)
val mHat = mt :/ (n.one - (b1 ** timestep))
val vHat = vt :/ (n.one - (b2 ** timestep))
val corr = c.learningRate *: (mHat / (vHat.sqrt + eps))
(corr, mt, vt)
layers
.zip(activations)
.foldRight(
List.empty[Layer[T]],
error,
None: Option[Tensor[T]]
) {
case (
(Layer(w, b, f, u, Some(AdamState(mw, vw, mb, vb))), Activation(x, z, _)),
(ls, prevDelta, prevWeight)
) =>
val delta = (prevWeight match
case Some(pw) => prevDelta * pw.T
case None => prevDelta
) multiply f.derivative(z)
val wGradient = c.clip(x.T * delta)
val bGradient = c.clip(delta).sum
// Adam
val (corrW, weightM, weightV) = correction(wGradient, mw, vw)
val newWeight = w - corrW
val (corrB, biasM, biasV) = correction(bGradient.asT, mb, vb)
val newBias = b - corrB
val adamState = Some(AdamState(weightM, weightV, biasM, biasV))
val updated = Layer(newWeight, newBias, f, u, adamState) +: ls
(updated, delta, Some(w))
case s => sys.error(s"Adam optimizer require state, but was:\n$s")
}
._1
The difference with classic gradient optimizer is:
timestepis an index across all training epochs and intermediate batches. Its range:[1 .. epochs * data.length / batchSize]correctionfunction that goes after Adam paper to calculate final learning rate based on the weight or bias gradient.- We keep Adam moments for weight and bias
AdamStateas part of the Layer state across all learning epochs.
There is an extension to Tensor API I have added to support element-wise operations like:
- division
def :/(that: T): Tensor[T] - multiplication
(t: T) def *:(that: Tensor[T]): Tensor[T] - power:
def :**(to: Int): Tensor[T] - square:
def sqr: Tensor[T] = TensorOps.pow(t, 2) - sqrt:
def sqrt: Tensor[T] = TensorOps.sqrt(t)
Visualisation
We are going to visualise Adam gradient trace to global minimum using Picta. So all we do is constructing ANN with Adam type parameter:
val ann = Sequential[Double, Adam](
meanSquareError,
learningRate = 0.0012f,
batchSize = 16,
gradientClipping = clipByValue(5.0d)
).add(Dense())
Loss surface:
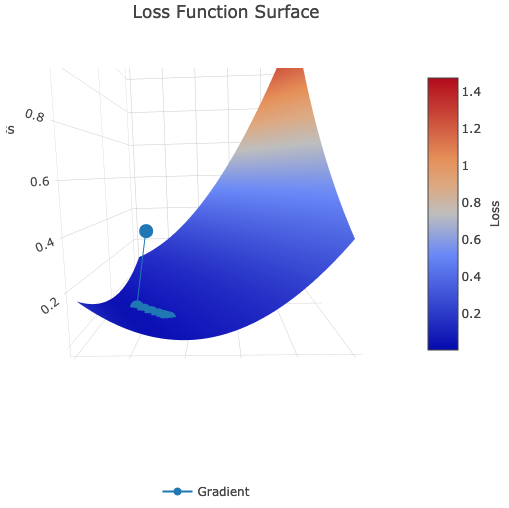
Also, we going to compare it on the same data with classic Gradient Descent:
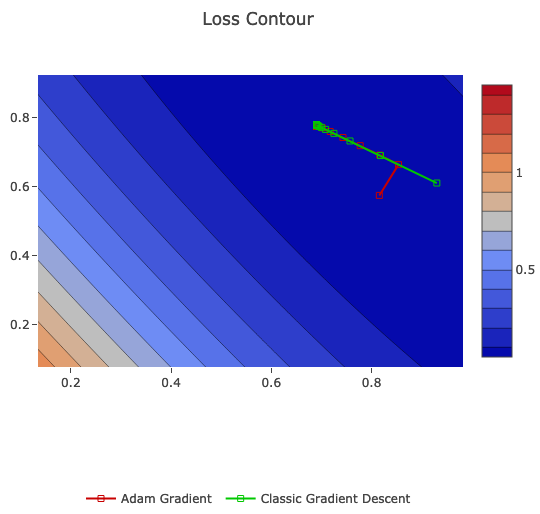
Adam gradient starts a bit differently then classic gradient descent. Eventually, they both converges at the same point.
If we compare the speed of finding global minimum, then on my data and on the same learning hyper-parameters, classic Gradient Descent is faster:
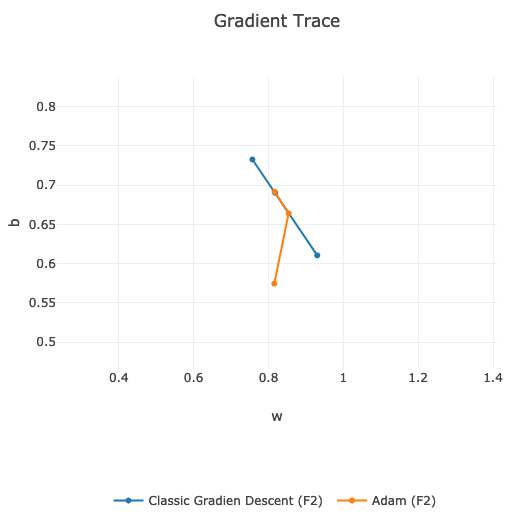
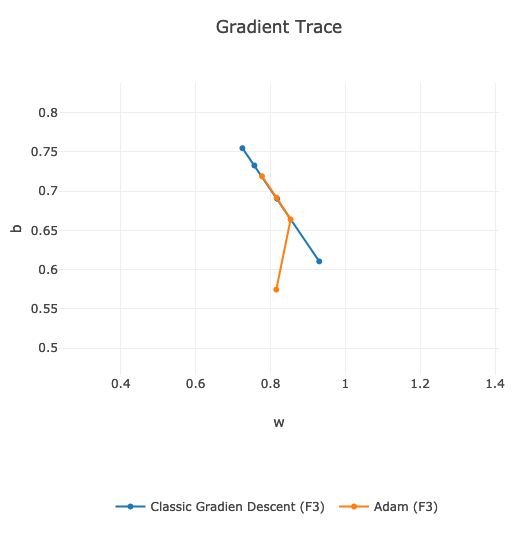
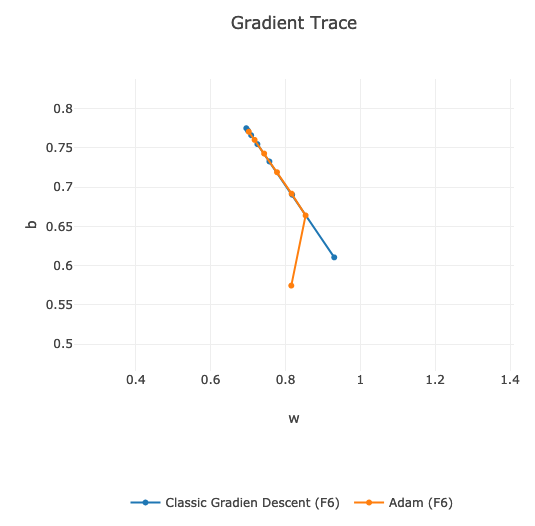
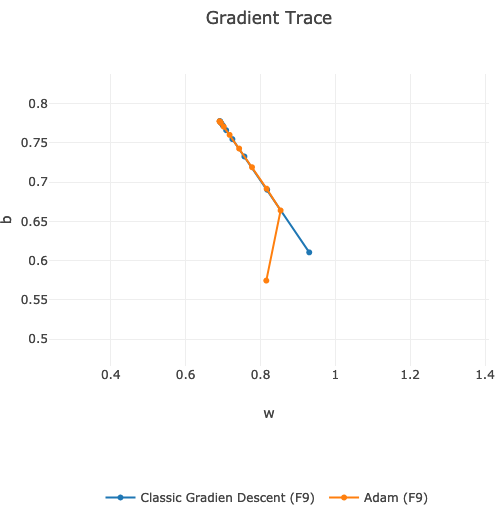
We can see that orange line is slightly behind the blue one. Around 9th learning epoch they are both in the same position.
Summary
We could easily extend existing library with one more optimizer such as Adam. It is quite popular optimizer nowadays as it shows good result in the paper and in practise. Anyway, it did not show better results on my data comparing to classic gradient descent algorithm. My experiment is not proving that Adam is not good, but it is just showing that in real life you need to experiment with different weight optimisers. Also, you should tune hyper-parameters for each algorithm separately, i.e. reuse of the same hyper-parameters might not help to get the best results out of another optimizer you are currently trying.