Decision Tree from scratch
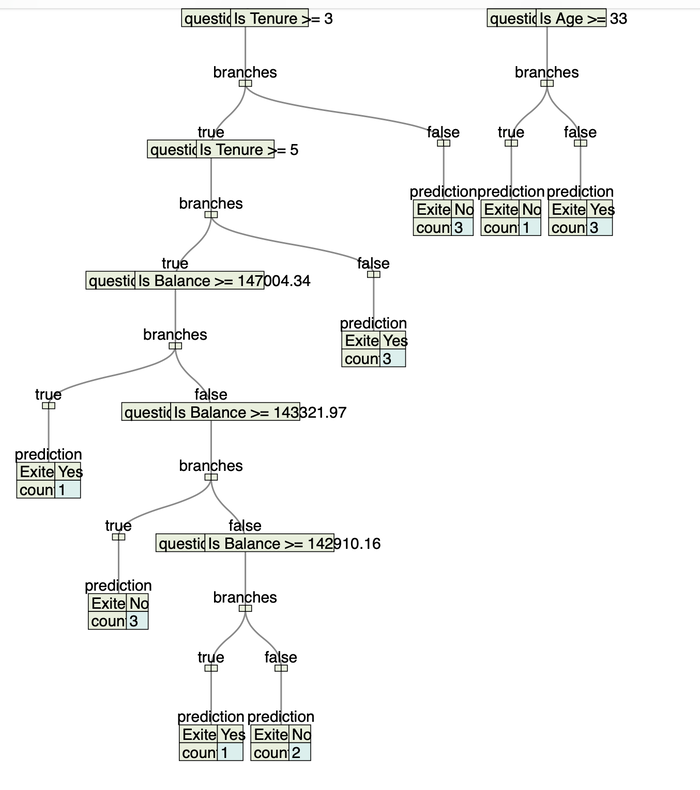
Cropped view of one the region in the middle of the tree we will build further

Decision Tree classifier is one the simplest algorithm to implement from scratch. One of the benefit of this algorithm is it can be trained without spending too much efforst on data preparation and it is fast comparing to more complex algorithms like Neural Networks. In this blog post we are going to implement CART algorithm, which stands for Classification and Regression trees. There are many other algorithms in decision trees space, but we will not describe them in this blog post.
Data science practitioners often use decision tree algorithms to compare their performance with more advanced algorithms. Although decision tree is fast to train, its accuracy metric usually lower than accuracy on the other algorithms like deep feed forward networks or something more advanced using the same dataset. However, you do not always need high accuracy value, so using CART and other decision tree ensemble algorithms may be enough for solving particular problem.
CART Algorithm
The whole algorithm can be described in several steps:
-
Building in-memory tree data structure based on input training tabular data:
a. Find the best split question to divide input rows into two branches
b. Repeat split for both branches recursively
-
Using in-memory tree data structure to classify unseen data samples.
Below is a decision tree in different scales we will build further. See a link to GitHub repo, which contains code store a decision tree as JSON file, so that you can visualize stoted JSON objects using any online JSON tree visualizer tool.
Fit-to-sreen view of further implemented decision tree:

Zoomed view to read some tree questions:
Building Blocks
We need several auxiliary data types to implement CART algorithms:
object Types:
// Label will be always a string type
type Label = String
// will support only 3 different types as data type for input features
type Data = Int | Float | String
// every sample row is an Array of Data
type Features = Array[Data]
// every sample row contains different features and target label
type Row = (Features, Label)
// input data structure is an array of array i.e. matrix
type Rows = Array[Row]
Decision Tree object will be built using the following types:
// contains column index and its column value at this index from the input data row
case class Question(col: Int, value: Data)
// recursive data structure
enum DecisionTree:
// contains predicted label and number of rows which are classified to a single label
case Leaf(predictions: Map[Label, Int])
// main building block that eventually terminates with `Leaf` nodes
case Node(
q: Question,
trueBranch: DecisionTree,
falseBranch: DecisionTree
)
Tree assembling
CART algorithm is using Gini impurity and Information Gain metrics in order to build efficient tree.
Gini impurity from Wikipedia:
Gini impurity (named after Italian mathematician Corrado Gini) is a measure of how often a randomly chosen element from the set would be incorrectly labeled if it was randomly labeled according to the distribution of labels in the subset.
Information gain from Wikipedia:
Information gain is used to decide which feature to split on at each step in building the tree. Simplicity is best, so we want to keep our tree small. To do so, at each step we should choose the split that results in the most consistent child nodes.
Let's encode this in programming language:
def classCounts(rows: Rows): Map[String, Int] =
rows.groupMapReduce(_._2)(_ => 1)(_ + _)
// math formula: 1 - Sum(p(i) ** 2), where i from 1 to J, J is number of classes
def gini(data: Rows): Float =
val counts = classCounts(data)
counts.keys.foldLeft(1f) { (impurity, label) =>
val labelProb = counts(label) / data.size.toFloat
impurity - math.pow(labelProb, 2).toFloat
}
def infoGain(left: Rows, right: Rows, currentUncertainty: Float) =
val p = left.length.toFloat / (left.length + right.length)
currentUncertainty - p * gini(left) - (1 - p) * gini(right)
In order to find the best question and make an efficient split for remaining rows, we need to implement a function like rows: Rows => (Float, Option[Question]).
The first member of the tuple is info gain:
def isNumeric(value: Data) =
value match
case _: String => false
case _ => true
// helper function to detect whether data sample macthes to a question, i.e. return true or false
def matches(q: Question, example: Features): Boolean =
val exampleVal = example(q.col)
if isNumeric(exampleVal) then
(exampleVal, q.value) match
case (i: Int, i2: Int) => i >= i2
case (f: Float, f2: Float) => f >= f2
case _ => false
else exampleVal == q.value
// helper function to partition rows by Question
def partition(data: Rows, q: Question) =
data.partition((features, _) => matches(q, features))
def findBestSplit(rows: Rows): (Float, Option[Question]) =
var bestGain = 0f
var bestQuestion = Option.empty[Question]
val currentUncertainty = gini(rows)
val featureCount = rows.headOption.map(_._1.length - 1).getOrElse(0)
for col <- 0 until featureCount do
val uniqueVals = rows.map((row, _) => row(col)).toSet
for value <- uniqueVals do
val question = Question(col, value)
val (trueRows, falseRows) = partition(rows, question)
// Skip this split if it doesn't divide the dataset.
if trueRows.nonEmpty && falseRows.nonEmpty then
// Calculate the information gain from this split
val gain = infoGain(trueRows, falseRows, currentUncertainty)
// You actually can use '>' instead of '>=' here
if gain >= bestGain then
bestGain = gain
bestQuestion = Some(question)
(bestGain, bestQuestion)
At this point we have all pieces to compose and get the CART algorithm done:
def leaf(data: Rows): Leaf =
Leaf(classCounts(data))
def buildTree(rows: Rows): DecisionTree =
val (gain, question) = findBestSplit(rows)
question match
case None => leaf(rows)
case Some(q) =>
if gain == 0 then leaf(rows)
else
// If we reach here, we have found a useful feature / value to partition on.
val (trueRows, falseRows) = partition(rows, q)
val trueBranch = buildTree(trueRows)
val falseBranch = buildTree(falseRows)
Node(q, trueBranch, falseBranch)
Decision Tree Classifier
In order to use built Decision Tree data structure we need one more function classify.
It goes through the tree by using input data sample until it reaches terminal Leaf node:
extension (node: DecisionTree)
def classify(input: Features): Map[String, Int] =
@tailrec
def loop(
input: Features,
node: DecisionTree
): Map[String, Int] =
node match
case Leaf(predictions) => predictions
case Node(question, trueBranch, falseBranch) =>
if matches(question, input) then loop(input, trueBranch)
else loop(input, falseBranch)
loop(input, node)
Demo on Custom Churn Dataset
We are going to use Customer Churn dataset, which I already used in Artificial Neural Networks blog post.
Input features of this dataset are:
CreditScore,
Geography,
Gender,
Age,
Tenure,
Balance,
NumOfProducts,
HasCrCard,
IsActiveMember,
EstimatedSalary
Let's load it from CSV file and split into two sub-sets for training and testing phases. Dataset consists of 10 000 data samples, so we get 8000 samples for training
and 2000 samples for testing:
def splitArray[T](
fraction: Float,
data: Array[T]
): (Array[T], Array[T]) =
val count = data.length * fraction
val countOrZero = if count < 1 then 0 else count
data.splitAt(data.length - countOrZero.toInt)
val textData =
DataLoader(Paths.get("data", "Churn_Modelling.csv")).load(3, -1)
val rows =
textData.data.map((features, label) =>
Array[Data](
features(0).toInt,
features(1),
features(2),
features(3).toInt,
features(4).toInt,
features(5).toFloat,
features(6).toInt,
features(7).toInt,
features(8).toInt,
features(9).toFloat
) -> label
)
val (trainData, testData) = splitArray(0.2, rows)
Using training data to build in-memory decision tree:
val classifier = buildTree(trainData)
Now we can use it to classify test dataset and calculate accuracy metric in the same time:
def accuracy(
classifier: DecisionTree,
data: Array[Row]
) =
data.map { (input, label) =>
val predictions = classifier.classify(input)
if predictions.contains(label) then 1f
else 0
}.sum * 100 / data.size
println(s"test accuracy: ${accuracy(classifier, testData)} %")
> test accuracy: 79.85 %
Program has been completed tree generation from training data and test data classification in roughly 10 seconds.
Accuracy on test data is 79.85 %. If we compare with ANN algorithm accuracy, which is 85.97 %, CART algorithm accuracy is worse.
Summary
We have implemented one of the decision tree algorithm CART, which is able to predict categorial or numeric target variable. This algorithm assembles tree data structure based on training data features by finding best question to ask for current set of data samples. Set of input data samples is getting smaller on every question split, so that all rows eventually get their predicted label. Once tree is built, we can use it to classify new data.
CART algorithm is easy to understand and it can be useful in certain data classification problems. This algorithm is fast and easy to train, since it does not require hyper-parameters or any other additional tuning techniques. It is also fast to train comparing to neural networks training efforts (GPU acceleration, lots of data, vanishing gradient).
If you need full project code, then check this GitHub repository:
https://github.com/novakov-alexey/decision-trees
The entire blog-post is based on this example: